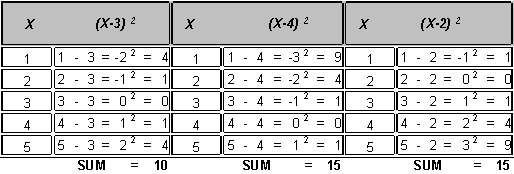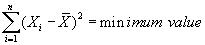|
The second property of the mean establishes that the sum of squared deviations from a distribution's mean will always equal a minimum value.
|
Written mathematically:
|
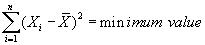
|
In other words, if we subtract the mean from every term in a distribution (creating the deviations from the mean), square these deviations, and then sum these squared deviations, the sum of squared deviations from the mean will always be the smallest possible sum of squared deviations. To illustrate, consider the following distribution (labeled X) whose mean is 3. First, we compute the squared deviations from the mean. Second, we compute the squared deviations from the constant 4. Third, we compute the squared deviations from the constant 2.
|